ICCV 2017 Tutorial

Covariance 2017

Venice - Sunday October 22

From Covariance Matrices to Covariance Operators:
Data Representation from Finite to Infnite-Dimensional Settings

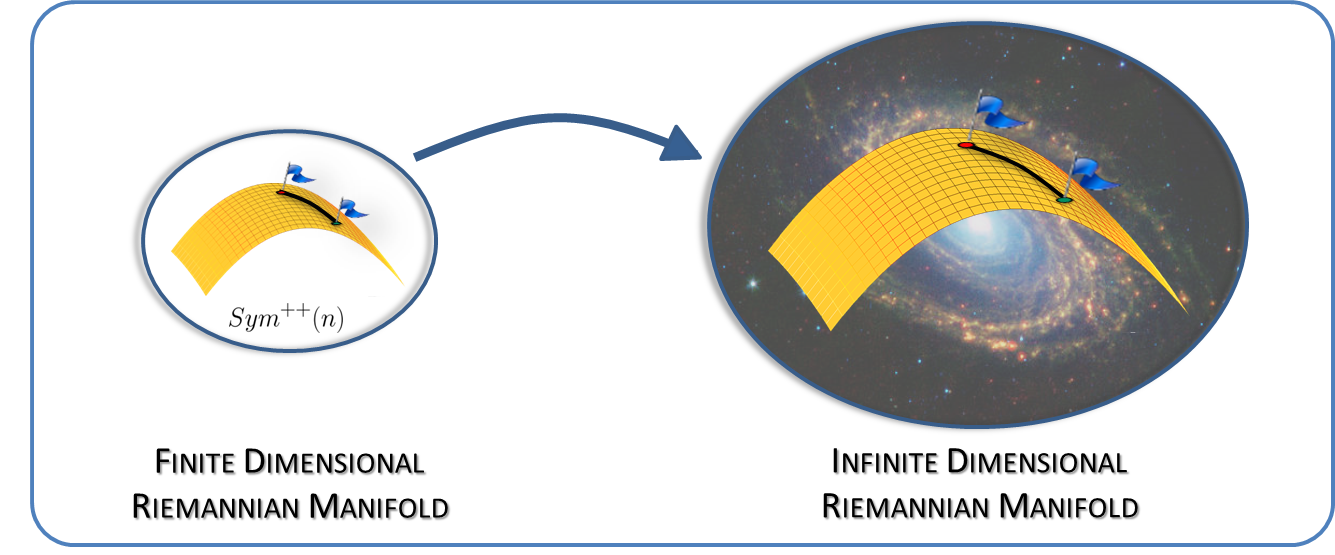This tutorial aims to provide an exposition to some of the recent developments in the generalization of the data representation framework using finite-dimensional covariance matrices to infinite-dimensional covariance operators in Reproducing Kernel Hilbert Spaces (RKHS). This direction combines the power of both kernel methods and Riemannian geometry and represents a promising avenue for future research, both methodologically and practically.
Symmetric Positive Definite (SPD) matrices, in particular covariance matrices, play an important role in many areas of mathematics, science, and engineering. In the field of computer vision and image processing, covariance matrices have recently emerged as a powerful image representation approach, commonly called covariance descriptor. In this approach, an image is compactly represented by a covariance matrix encoding correlations between different features extracted from that image. This representation has been demonstrated to work very well in practice and consequently, covariance descriptors have been successfully applied to many computer vision tasks, including people tracking, object detection and classification, action recognition, face recognition, emotion recognition, person re-identification, and image retrieval.
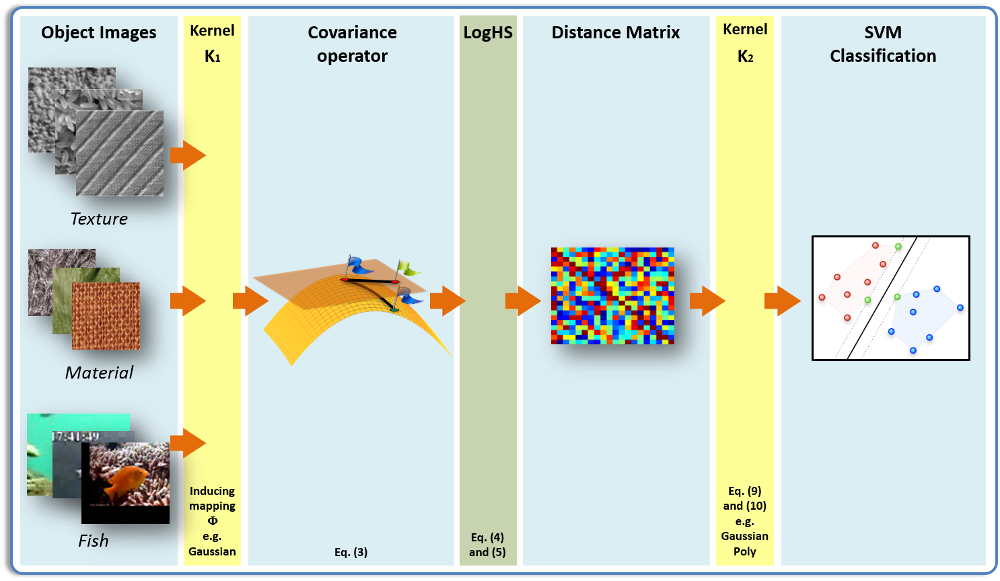While they have been shown to be effective in many applications, one major limitation of covariance matrices is that they only capture linear correlations between input features. In order to encode nonlinear correlations, we generalize the covariance matrix representation framework to the infinite-dimensional setting by the use of positive definite kernels defined on the original input features. Intuitively, from the viewpoint of kernel methods, each positive definite kernel, such as the Gaussian kernel, induces a feature map that nonlinearly maps each input point into a high (generally infinite) dimensional feature space. Each image is then represented by an infinite-dimensional covariance operator, which can be thought as the covariance matrix of the infinite-dimensional features in the feature space. Since the high-dimensional feature maps are nonlinear, the resulting covariance operators thus encode the nonlinear correlations between the original features in the image.
The set of SPD matrices is a not vector subspace of Euclidean space under the standard matrix addition and scalar multiplication operations, but is an open convex cone that also admits a smooth manifold structure. Consequently, in general, the optimal measure of similarity between covariance matrices is not the Euclidean distance, but a distance that captures the intrinsic geometry of SPD matrices. Among the most widely used non-Euclidean distances for SPD matrices are the classical affine-invariant Riemannian distance, the recently introduced Log-Euclidean distance, and the distance-like Bregman divergences. All of these distances and divergences have recently been generalized to the infinite-dimensional setting. In the case of RKHS covariance operators, they admit closed form formulas via the corresponding Gram matrices. For large scale data sets, which require the handling of large numbers of covariance operators, these distances and divergences can be approximated by kernel approximation methods. Using the Log-Euclidean distance and its infinite-dimensional counterpart, the Log-Hilbert-Schmidt distance, one can define positive definite kernels, such as the Gaussian kernel, allowing kernel methods to be applied directly on the manifold.